Z Score Interpretation: Z-score is a part of statistics and today it is used in finance, accounting, healthcare, businesses, etc. Z score is defined as the estimation of how many standard deviations a data positions from the mean. Another name for the z-score is the standard score.
If you want to calculate Z Score then here is the link: Z Score Calculator
Z Score Interpretation with Solution
How to Calculate Z-score:
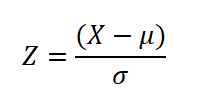
Where,
X is the raw data score value.
μ is the mean of the total given data set.
σ this sign indicates the standard deviation of the given data set.
Illustration of z-score:
- If the z-score value is 0 then the data position value is accurately at the mean of the data values.
- If the z-score is greater than the mean value or falls above the mean value, it is called a positive z-score.
- Contrarily, if the z-score is lesser than the mean value or drops below the mean value, it is called a negative z-score.
Let us understand the z-score by taking a real-time scenario,
Example:
Abeera is a data analyst at a little retail store. Her manager has observed changes in employee performance in different departments and wants to know the basic factors presenting these differences. The manager wants to identify patterns in employee performance metrics such as sales revenue, customer satisfaction scores, and hours worked, and determine if there are any significant changes between departments.
Solution:
Let us assume that Abeera collects performance metrics of two different departments that are Department P and Department Q, that data includes sales revenue, customer satisfaction scores, and hours worked for every employee over the last month. After gathering the data Abeera started analyzing,
Abeera uses the Z-score formula to calculate each performance metric,
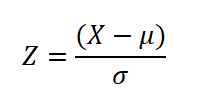
The employee performance analysis table that Abeera has analyzed
| Department | Employee ID | Sales Revenue | Customer satisfaction | Hours Worked |
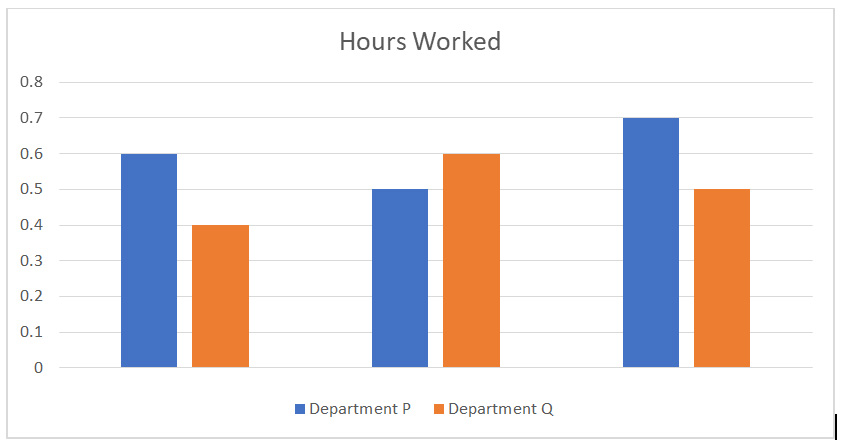
| P | 001 | 0.8 | 0.7 | 0.6 |
| P | 002 | 0.6 | 0.6 | 0.5 |
| P | 003 | 0.7 | 0.8 | 0.7 |
| Q | 101 | 0.5 | 0.6 | 0.4 |
| Q | 102 | 0.4 | 0.5 | 0.6 |
| Q | 103 | 0.6 | 0.4 | 0.5 |
In the above table, Z-score columns include sales revenue, customer satisfaction scores, and hours worked.
Abeera has calculated the Z-score of each department and compared it with each other if the Z-score value of department P has a consistently higher score for sales revenue compared to department Q, it indicates that better sales performance in department P.
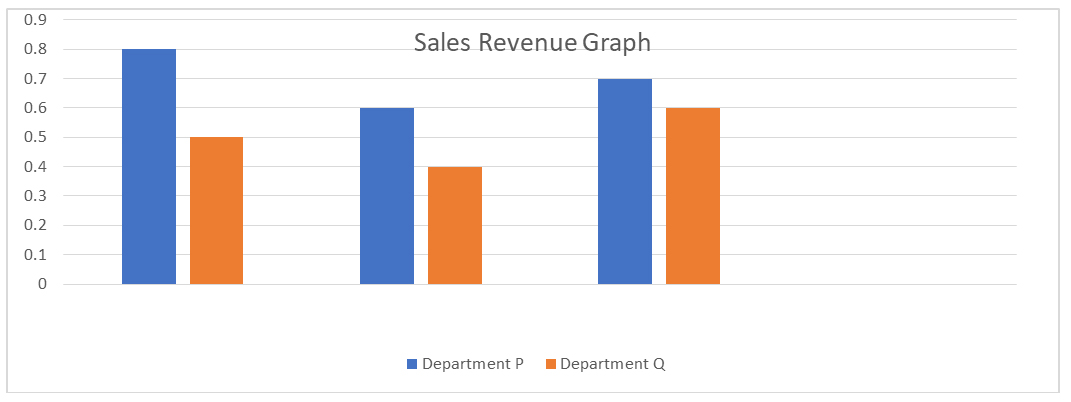
Graphical representation of sales Customer satisfaction of both departments
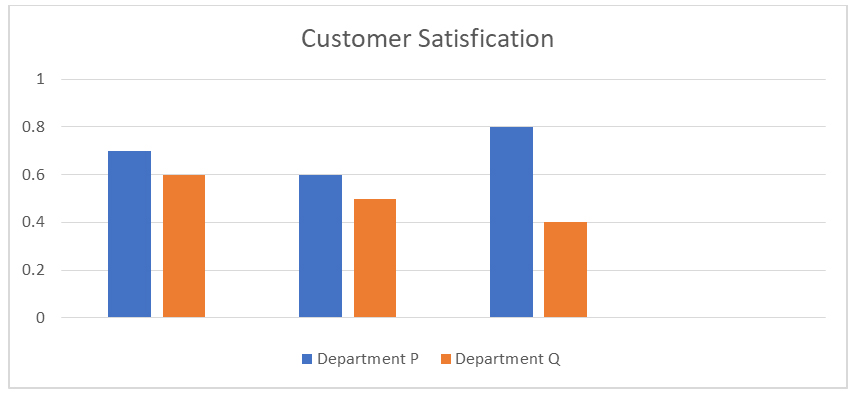
Graphical representation of sales Hours worked by both departments
Why do we use the Z-score?
As we have seen in the above example z-score allows meaningful comparison between different values by standardization. It also allows us to find out the extreme values or outliers which can provide valuable results from the datasets.
Z-score makes it easy to interpret data by providing straightforward values by indicating how many standard deviations a data position is away from the mean.
Benefits:
- Z-score allows us to relate various datasets even if they have different scales or units.
- It is widely used in different fields for statistical analysis of data and makes it easier to interpret and get the results from the data.
Limitations:
- Z-score is an assumption-based calculation, as you have seen in the above example it may not be appropriate in many scenarios.
- Z-score sometimes provides standard values measuring and interpreting their values might be a complex task.
Applications of Z-score:
- Z-score is used in many fields like finance for risk analysis and financial conclusion analysis, healthcare for medical diagnosis and clinical trials, education, Sports and market analytics etc.
The Z-score is a powerful mathematical mechanism that helps in analyzing and interpreting data in various fields.
Our Other Calculators