Permutations and combinations are the two important topics of mathematics and these two topics hold distinct meanings and applications and are crucial to understand various concepts of mathematics such as probabilities.

Let us imagine an event where two best friends Sia and Eda are invited to a Halloween party. They can have unique and awesome costumes, but there is a twist in the event they both can wear whatever costume they want but they have to wear masks with different colors and shapes. But here is a small problem, does it matter which mask each of them wears (order)? Or just they all have different color and shape masks(selection)?
If you want to calculate Permutation and Combination then here is the link: Permutation and Combination Calculator
The answer depends on whether you are choosing permutations or combinations to solve the problems. If you choose permutation then you should know permutations care more about order like figuring out different prize flight tickets and if you choose combination then it care more about selection just like selecting different flavors for your ice cream.
What Is The Difference Between Permutation And Combination?
Before moving to the differences let us understand the definitions of Permutations and combinations.
Permutations:
Permutation is the process of arranging objects or elements in a particular order.
The formula which is used to calculate the permutations:
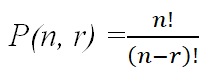
Where,
- n is the total number of objects or elements given.
- r is the number of objects or elements meant to be arranged.
- n! defines the factorial of n, which is the yield of all positive integers up to n.
Example: Let us imagine having 5 different books P, Q, R, S, T and you want to arrange 3 books on a shelf. Calculate the number of permutations.
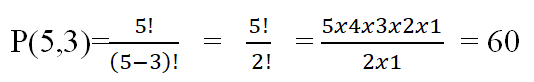
Therefore, there are 60 different ways to arrange 3 books out of 5 on a shelf.
Combination:
Combination is the process of selecting elements or objects without considering their order.
The formula which is used to calculate the combination:
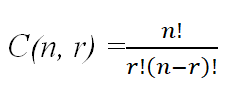
Where,
- n is the total number of objects or elements given.
- r is the number of objects or elements meant to be arranged.
- n! define the factorial of n, which is the yield(product) of all positive integers up to n.
- r! represents the factorial of r, which is the yield (product) of all positive integers up to r.
- (n-r)! represents the factorial of n-r, which is the yield (product) of all positive integers up to n-r.
Example:
Let’s imagine that you are a teacher and you have 7 students and want to form 4 student groups for school activities. What are the number of combinations that can be calculated?
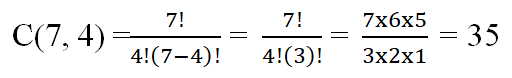
Therefore, there are 35 different combinations of selecting 4 students out of 7 for school activities.
Here are the differences between the permutations and combinations
| PERMUTATIONS | COMBINATIONS |
| It is the process of arranging the elements or objects. | It is the process of selecting the elements or objects. |
| In permutations order is important. | In combinations, order is not an important aspect. |
| It is symbolized as nPr | It is symbolized as nCr |
| In this, each arrangement will be unique. | Different arrangments may get the same combination. |
| The permutation concept is most commonly used in Probability and statistics. | The combination concept is most commonly used in combinatorial problems. |
| It is used in solving problems involving sequences and arrangements. | It is used in solving problems involving selections and combinations. |
| Repeated selection of objects or elements is not allowed. | Repeated selection of objects or elements is allowed. |
| The number of outcomes is generally larger. | The number of outcomes is generally smaller. |
| Examples such as scheduling tasks, seating arrangements, races, etc. | Examples such as team formation, lottery picks, and flavor combinations. |
Permutations and combinations are the two powerful mechanisms for arranging and selecting objects or elements. By understanding the key differences between the permutations and combinations you will be able to choose the right approach to solve problems. Permutations help us to arrange elements in an orderly manner, whereas combinations allow us to select the elements without considering the order. Permutations and combinations play important roles in making informed decisions at various stages of our lives.
Our Other Calculators